Intro

When you look at a photograph, your brain instantly infers which objects are near or far - even though the image itself is flat. Machines don’t have this innate ability. Monocular depth estimation teaches computers to infer depth using just one camera, without stereo vision or LiDAR. In this post, we’ll explore how it works, why transformers have transformed the field, and how it can be deployed efficiently on small edge devices.

1. Why Depth Matters

Depth is at the heart of perception. Robots use it to navigate, AR systems use it to place objects correctly, and self-driving cars rely on it for safety. At Hoomanely, depth helps our smart bowls and cameras understand pet behavior - posture, movement, and interaction - without requiring multiple sensors.

Traditionally, depth came from stereo cameras or LiDAR, which depend on geometry or active sensing. Monocular estimation achieves similar results by learning depth cues from a single image.

2. How One Image Encodes Depth

A single image encodes subtle hints of depth:

• Perspective: Distant lines appear to converge.
• Relative size: Familiar objects appear smaller when farther away.
• Texture and blur: Details fade with distance.

These cues are the same principles your brain uses when looking at a photograph. In computer vision, these relationships are captured mathematically.

Formula 1 – Perspective Relation

h_i / H_i = f / Z_i

This formula comes from the pinhole camera model. It means that an object's apparent height on the image (h_i) is proportional to its true height (H_i) and the focal length (f) of the camera, and inversely proportional to its distance from the camera (Z_i).

In simpler terms: the farther an object is, the smaller it appears on the image.

Rearranging this gives:

Z_i = f * (H_i / h_i)

So, if we know the camera's focal length and the actual size of an object, we can estimate how far it is. Of course, in real scenes, we rarely know the true size of every object - which is why machine learning comes in.

Formula 2 – Mapping from Image to Depth

F: I(x, y) -> D(x, y)

Here, the network learns a function F that maps each pixel’s intensity (I) to a corresponding depth value (D). Instead of relying on exact geometry, it learns from data: seeing many images with known depths and internalizing those relationships.

3. From CNNs to Transformers

Early models used Convolutional Neural Networks (CNNs) to infer depth locally - they scanned small image patches and pieced together the larger scene. These networks captured fine details but often failed to connect distant parts of an image, like how the horizon and nearby objects relate.

To improve learning, researchers introduced self-supervised training, where depth is learned by reconstructing one camera view from another:

L_photo = | I_L - I_R^warp(D) |

This formula represents a photometric reconstruction loss. The model predicts depth D, uses it to warp one image view (I_R) to match another (I_L), and minimizes the difference between them. If the reconstruction looks correct, the depth prediction is likely accurate. It allows learning depth without needing labeled data.

Then came Transformers, which changed everything. Instead of processing small patches in isolation, transformers reason globally using self-attention:

Attention(Q, K, V) = softmax((QK^T) / sqrt(d_k))V

Here, each pixel (represented as a query Q) interacts with every other pixel (keys K and values V), learning how strongly they influence one another. This means the network can understand how distant regions in the image are related - for example, how the brightness of the sky might affect the shading of the ground.

Transformers also learn object size priors: they recognize that people, cars, or furniture usually have certain sizes, and use this knowledge to infer relative distance. While this brings impressive realism, it can sometimes confuse scale (a toy car might be read as a far-away real one). Overall, by combining global reasoning with semantic understanding, transformers produce smoother, more coherent depth maps.

4. Training and Deployment

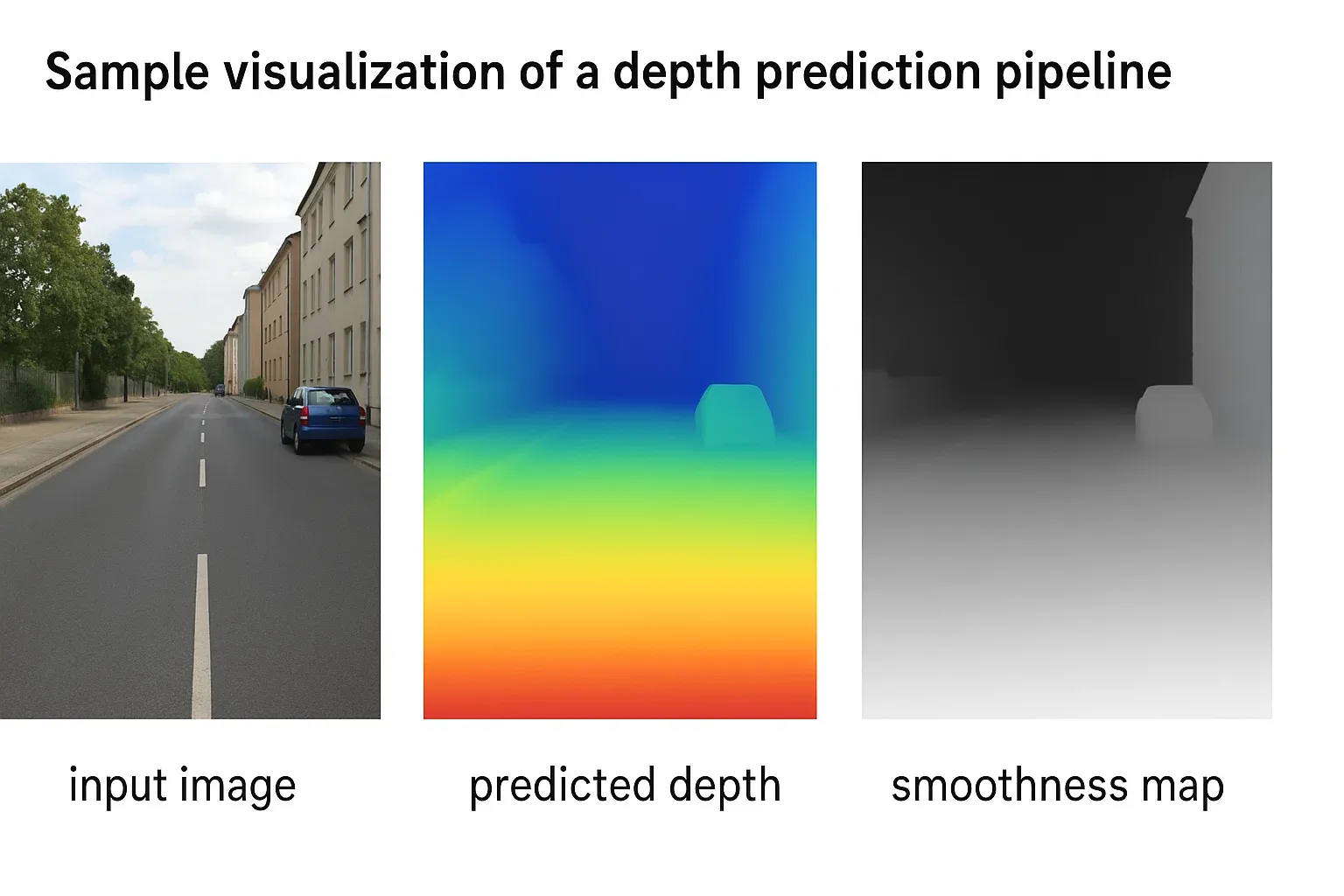
Depth models are trained on datasets where each pixel’s true depth is known, such as NYU Depth V2 (indoor environments) and KITTI (outdoor driving). The goal is to make predicted depths accurate and smooth across surfaces:

L_total = Mean(|D - D*|) + λ * |∇D|

This is the total loss used in training.

• The first term (|D - D*|) is a pixel-wise loss, ensuring each predicted depth value is close to the ground truth.
• The second term (|∇D|) is a smoothness loss, encouraging neighboring pixels to have similar depths so that flat surfaces remain smooth.
• The coefficient λ balances how much we care about accuracy versus smoothness.

This helps the model predict depth maps that are both correct and visually natural.

When deploying on edge devices, efficiency matters as much as accuracy. Several techniques make this possible:

• Distillation: A smaller “student” model learns from a large, accurate “teacher” model.
• Quantization: Reduces 32-bit model weights to 8-bit without major accuracy loss.
• Pruning: Removes redundant or unused connections to shrink model size.

These optimizations allow modern models like MiDaS to infer depth at around 15 frames per second on a Raspberry Pi, effectively turning a simple camera into a 3D sensor.

5. Limitations and the Road Ahead

Monocular depth estimation is powerful but not perfect:

• Scale ambiguity: The model struggles with absolute distances since a small object up close can look like a big object far away.
• Reflective and transparent surfaces: These confuse the model because reflections distort light cues.
• Temporal inconsistency: When processing video, predictions can flicker between frames.

The next generation of research combines monocular depth with Neural Radiance Fields (NeRFs) and diffusion-based 3D reconstruction, bridging the gap between 2D learning and 3D geometry. These hybrid methods integrate physical consistency with learned priors, bringing depth estimation closer to how humans perceive space.

Key Takeaways

• Monocular depth estimation extracts 3D understanding from a single image.
• Transformers outperform CNNs by reasoning globally and learning object priors.
• Edge optimizations like distillation and quantization enable real-time use.
• Future models will merge semantic and geometric depth reasoning for greater accuracy.